안녕하세요. 이번에는 무엇을 할까요? polyphase representation 을 이용해서 DFT를 표현해보도록 하겠습니다. polyphase representation 을 이용하면 이것 저것 할 수 있습니다. 이제 얘기를 해볼까요.
polyphase representation 을 이용한 DFT filter bank
DFT filter bank
우선 DFT filter bank에 대해 알아보겠습니다. DFT filter bank의 Filter 들은 아래와 같이 생겼습니다.
$$H_k(z) = H_0(zW^k)$$
여기서 $H_0$를 이용해서 다른 필터들을 정의하죠. 그러면 우선 $H_0$ 를 분석해야 겠죠. $H_0$의 polyphase representation에 대해 알아보겠습니다.
$H_0$의 polyphase representation
$H_0$의 polyphase representation 은 아래와 같습니다.
$$H_0(z) = \sum_{l=0}^{M-1} z^{-l}E_l(z^M)$$
DFT filter bank 표현
위에서 polyphase representation 을 바탕으로 아래와 같은 식이 유도 되죠.
$$H_k(z) = H_0 (zW^k) = \sum_{l=0}^{M-1} (z^{-1}W^{-k})^l E_l (z^M)$$
만약에 여기서 $E_l(z)=1$이라면 uniform DFT filter bank 가 됩니다.
DFT filter bank 와 decimation
만약에 DFT filter bank 의 output 이 $M$만큼 decimation 된다면 noble identity 에 의해 아래와 같이 표현 할 수 있습니다.
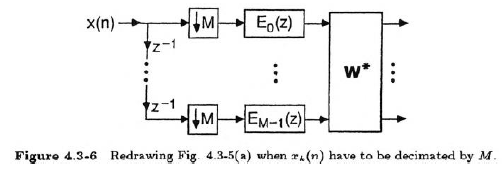
phase representation 을 하면 좋은 이유
DFT filter bank를 phase representation 이용해서 표현하면 좋은 이유는 뭘까요? $H_0(z)$를 frequency selective filter 역할을 하도록 만들 수 있습니다.
그림 및 내용출처
-

댓글